PMC Logo

    Review of:
    Arkady Plotnitsky, The Knowable and the Unknowable: Modern Science, Nonclassical Thought, and the "Two Cultures." Ann Arbor: U of Michigan P, 2002.

  1. In The Knowable and the Unknowable, Arkady Plotnitsky takes on (at least) two unenviable double tasks. He endeavors to explain to nonexperts the rationally necessitated departure from traditional visual representation that, in part, characterizes "modern" or "nonclassical" physics and mathematics while--equally if not more arduous to achieve--distinguishing and defending groundbreaking philosophical reflection from the scattershot of slighter minds. In addition, rather than succumb to the ready pleasures of polemic in carrying out these aims, he carefully provides, in his own writing, an example of intellectual scrupulousness so striking as to inspire the improbable hope that The Knowable and the Unknowable might set a discursive benchmark to which less circumspect commentators may one day rise. Finally, Plotnitsky does all this while managing to avoid the fate to which his theoretical expertise and abilities could easily condemn him, that of being hamstrung by his own level of understanding, tied down, or compelled to talk down, like a Gulliver captive among the uncomprehending.

  2. Such discrepancy of stature is both the inspiration for and subject matter of Plotnitsky's project. While describing and addressing cognitive issues of historic and (literally) immeasurable scope, The Knowable and the Unknowable also represents and responds to a tempest in a teapot, a battle in print of truly Swiftian disproportion: the recent controversy regarding the supposed use and abuse of science by contemporary theorists and philosophers. The so-called "Science Wars" in which Plotnitsky intervenes were inaugurated by Paul R. Gross and Norman Levitt's Higher Superstition: The Academic Left and Its Quarrels with Science, but were brought to popular attention under the spotlight of scandal with the publication of Alan Sokal's "Transgressing the Boundaries--Towards a Transformative Hermeneutics of Quantum Gravity" in Social Text. The uproar it caused stemmed not from the content of the "transgression" that Sokal's article nominally proposed but from the fact that its proposal for publication received approbation at all. Following squarely in the tradition of discursive interaction that J. L. Austin named "speech acts," whose uncircumscribable, working principle the author of the action entitled "Transgressing the Boundaries..." would perforce disavow, Sokal's article was less about what it said than what it did. And what it did was speak double talk to great effect, perpetrating a hoax which the editors of Social Text "failed" to recognize as such (the general failure of quiddity in the face of effectivity, or at least their nonidentity, being what speech-act theory is all about). Sokal "successfully" presented what, in his view, would constitute a poststructuralist view of quantum physics, travestying both contemporary theory and quantum physics to achieve that pragmatic end. One year later, buoyed by his imposture, he joined forces with Jean Bricmont to publish Impostures intellectuelles, subsequently translated into English as Fashionable Nonsense: Postmodern Intellectuals' Abuse of Science. In the interim, Nobel-prize-winning physicist Steven Weinberg reflected on "Sokal's Hoax" in The New York Review of Books, followed by "Steven Weinberg Replies" and "Sokal's Hoax: An Exchange," and Plotnitsky and Richard Crew engaged in their own "exchange" on the "Wars" in the pages of this journal.

  3. For the active wagers of the "Science Wars," however, the de facto inauguration of hostilities took place long before their own maneuvers, with a tentative answer by Jacques Derrida to a question posed to him at a conference at Johns Hopkins University in 1969. The proceedings of that watershed event, compiled into the now-classic volume The Structuralist Controversy by editors Richard Macksey and Eugenio Donato, include contributions from and exchanges among many of the leading theorists of two generations working in Europe and America (then and now). As the title of the volume indicates, these historic discussions occurred previous to the coining of the catch-all chronological denomination "poststructuralism." Heterogeneous, neither "structuralist" nor identifiably anything else, they in large part exposed for the first time, at least in the U.S., the prospect of modes of thinking as yet undesignated and unknown, work so different as to correspond to no available proper designation.

  4. Theoretical work that deliberately detaches itself from any governing concept may, by force of its own unsubordinated status, occasion its comparison with other concepts and conceptual work. In focusing on the uncertain epistemological status of discourse committed to pursuing adequate representations of truth without proffering new abstractions or representations of truth in their place, such theoretical writing seems both to pose and to beg the question of its own internal understanding. Like the cognitive problems and impasses in the writing it analyzes, theoretical discursive analyses may have the effect of suggesting that, by other means, their purposeful conceptual lacunae may be filled, that the persistent variable, or unknown, they indicate, may be defined by way of analogy or equation. Such suggestibility, if encountered in good faith, leads to questions of the most basic and probing nature: if one cannot name or say what x is, say, that x equals y, then can one say, at least for the time being, that x is something like y?

  5. Such a searching question was improvised at the Johns Hopkins University Conference by an important interpreter of Hegel, the late Jean Hyppolite, in response to the paper "Structure, Sign, and Play," presented by Derrida. Hyppolite briefly asked that Derrida consider any similarities between his own destructuring work in the domain of philosophical systems and concepts and Einstein's theory of relativity. Derrida's equally brief response suggests that a similarity between the two indeed exists. Now, in the five-decade history of Derrida's discursive work--exacting, often transformative excurses on philosophical and literary writings revealing both the indissoluble relationship of the stated and implicit purposes and problems of these writings to "writing" as such (that is, as nonconceptual, iterable, and recognizable material form) and the systematic vocabularies, figures, and conceptual frameworks or limits in which these problems and purposes are posed--this tentative answer to Hippolyte stands alone. Derrida has made no more extensive comparison between his own analyses of the cognitive and representational difficulties posed in and by writing aiming at knowledge (whether of the abstract, conceptual, or philosophical, or of the "real," concrete, or referential kind), and the radical transformation by modern science and post-Euclidian mathematics of how we know and thereby what we know of the physical "world." The lone existence, in an extraordinarily prolific career, of a single, halting statement of fewer than sixty words produced spontaneously in answer to the suggestion of another only underscores the obvious about the adversarial posture into whose aegis it has been inverted: that the "Science Wars," whatever that appellation means and whatever is meant to be won by them, have not exactly been joined with any appreciable degree of reciprocity; in short, that these are "wars" waged by one side alone.

  6. A "war" waged by one side, one may argue, is an attack--in this instance an attack that, lacking even a substantive pretext, fabricates its own dummy text, a hoax--and Plotnitsky is unusually capable of defending those individual developments in philosophy, now dubbed "poststructuralist" by default, which are less antagonistic to than allied with those developments in physics and mathematics he helpfully calls "nonclassical" (xiii et passim). Trained as a mathematician first and a literary theorist second, Plotnitsky's perceptions and intellectual development reverse the direction of untoward, misleading appropriation ascribed to discursive theorists by the wagers of the "Science Wars"--most prominently, to Derrida and Lacan, and synecdochically, or, perhaps, simply cynically, to all contemporary theoretical work. While scientist-warriors may view nontraditional philosophers and theorists as poachers upon the "hard" disciplines seeking to inflate and buttress their own insubstantial prestige, Plotnitsky instead finds in nontraditional philosophy a wrestling, from within the bounds of discourse, with the formal and empirical boundaries that gave rise to non-Euclidian mathematical theory and quantum mechanics. For Plotnitsky, the problems of the limits of cognition, whether discursively or mathematically conceived, are problems of rational or commensurate representation any and all disciplines fundamentally interested in the bases and emergence of knowledge must share.

  7. The overlap between empirical and theoretical knowledge is rarely, if ever, complete, and mathematical inquiry, since the invention of geometry, has often served as a self-sustaining bridge between them. The symbolic language of mathematics is a language of self-evidence, which is to say, a language unlike language, and its adoption in the study of physical data and relations frees science of some of the limits and errors that accompany experiment and perception. Still, scientists in even the most mathematically rich domains do engage in productive discord among themselves; the names Einstein and Bohr stand for one such signal development in twentieth-century atomic physics, as do the diverging yet, of course, interrelated paths taken by their early modern counterparts, Descartes and Leibniz. Indeed, if one wanted to locate a real passing referent for the unfortunate denomination "Science Wars," perhaps one would do well to look first to its prima facie significance, the disputes within science itself. For what we understand and designate as "science" at any one time is the product of an ongoing history of differing interpretations, intellectual orientations, and directions, the often mutually contradictory or only partly shared views of physical reality whose full or partial, independent or contingent approbation may be immediate or delayed, refuted or maintained.

  8. The interpretive antagonisms and contradictions composing the progress of science were taken to another power--squared, or contradicted as contradictions themselves--when Bohr proposed that, at the atomic level, experimental results that appeared mutually exclusive should be considered "complementary." In The Knowable and the Unknowable, as in his earlier Complementarity: Anti-Epistemology after Bohr and Derrida, Plotnitsky follows Bohr to the heart of the "logical contradiction" (66) that is the consequence and insight of quantum physics, namely, that our only empirical means for knowing "quantum objects" (67) destructure that knowledge even as they structure it, linking the known (for example, the "particle" or "wave" appearances of light) directly to the unknowable (how and why such dual appearances indeed take place and pertain to a single phenomenon). The conjunction of quantum objects and their science yields a kind of knowledge that is neither the antithesis of ignorance nor its cancellation and replacement, but its necessary while never observably continuous complement. Plotnitsky's elucidating summary and discussion of the "double-slit experiment"--by which particles such as electrons or photons passing through screens with slits in them produce or do not produce a wave-like pattern depending on whether a detector of their movements, external to the movements themselves, is used in the experiment (61-66)--makes this paradox of empirical, experimental, or contingently objective knowledge clear:

    9. if [...] there are counters or other devices that would allow us to check through which slit particles pass (indeed even merely setting up the apparatus in a way that such a knowledge would in principle be possible would suffice), the interference pattern inevitably disappears. In other words, an appearance of this pattern irreducibly entails the lack of knowledge as to through which slit particles pass. Thus, ironically (such ironies are characteristic of or even define quantum mechanics), the irreducible lack of knowledge, the impossibility of knowing, is in fact associated with the appearance of a pattern and, hence, with a higher rather than a lower degree of order, as would be the case in, say, classical statistical physics. (64)

  9. Particles which seem to know more about our behavior (whether we've set up a detector or not) than we do about theirs (how do they "know that both slits are open, or conversely that counters are installed, and modify their behavior accordingly?" [66]) present, at very least, a "situation [...] equivalent to uncertainty relations" (64), if not a necessary suspension of logical and causal assertions of any classical kind. Yet Bohr's Copernican shift consisted in viewing differently not the fact of these antagonistic results, but rather the way in which we view their (mutually exclusive) factuality. It is not what we see but how we think of what we are seeing, the way in which we define and understand a quantum object--as a thing with certain attributes in itself or a "whole" constituted of experimentally conditioned, individual, phenomenal "effects"--that Bohr's view changes. Quantum mechanics--on Bohr's "interpretation" (68-69)--requires, in the first place, a different mode of interpretation, and Bohr's name for that different view of what quantum evidence means is "complementary." As Bohr describes it in the "Discussion with Einstein":

    10. evidence obtained under different experimental conditions cannot be comprehended within a single picture, but must be regarded as complementary in the sense that only the totality of the [observable] phenomena [produces the data that] exhausts the possible information about the [quantum] objects [themselves]. (70)

  10. While originating in a predicament produced by physical experiments (set up as means of clarification), Bohr's loosening of the logician's double bind is conceptual in kind. As Plotnitsky observes, the introduction of the term "complementary" with regard to quantum mechanics enacts an epistemological shift from "objectivity" to "effectivity," based upon, rather than stymied by, mutually exclusive, experimental results:

    11. thus, on the one hand, quantum objects are (or, again, are idealized as) irreducibly inaccessible to us, are beyond any reach (including again as objects); and in this sense there is irreducible rupture, discontinuity, arguably the only quantum-physical discontinuity in Bohr's epistemology. On the other hand, they are irreducibly indissociable, inseparable, indivisible from their interaction with measuring instruments and the effects this interaction produces. This situation may seem in turn paradoxical. It is not, however, once one accepts Bohr's nonclassical epistemology, according to which the ultimate nature of the efficacity of quantum effects, including their "peculiar individuality," is both reciprocal (that is, indissociable from its effects) and is outside any knowledge or conception, continuity and discontinuity among them [...] Thus Bohr's concept of the indivisibility or (the term is used interchangeably) the wholeness of phenomena allows him both to avoid the contradiction between indivisibility and discontinuity (along with other paradoxes of quantum physics) and to reestablish atomicity at the level of phenomena. (70-71)

    Like discourse, one could say, the effectivity of atomic objects is dependent but unlimited, contingent upon the interrelated experiments of which it is a result rather than derivative of the object in itself. Like rhetoric as such, rather than the specific rhetorical notion of the symbol or symbolon, according to which image and idea match, puzzle-like, to compose a single, concretely expressive meaning, Bohr's interpretation and use of the term "complementary" do not signify an integral meshing of categorically distinct entities. The "aspects" or "characteristics" of atomic "phenomena" are what we "know"--in Bohr's nontraditional phenomenological sense--but those aspects are derivative of the different experiments to and by which atomic objects are exposed (in rhetorical terms, these would be the different formulations or linguistic experiments that make evident different aspects of discourse, such as figure, noun, sign, or, following Saussure--surely, the Bohr of language study--signifier). A notion of the complementary that is not, or is only temporarily, contingently, closed, is, Plotnitsky points out, "peculiar" (74). Yet such peculiar language use may indeed be exactly appropriate to Bohr's epistemology. For, like the nonsynthetic relations it describes, the name of Bohr's interpretive breakthrough breaks the mold--the mold of the commensurate and thus traditionally "complementary" parts of a whole symbolized in rhetoric by the notion of the symbol, the equation and union of two as one. Bohr's notion of "complementarity" instead fractures a delimited object of investigation, normally identified through a series of equations, into experimental "phenomena" whose perceptibility consists in a series of differing effects. Furthermore, this fracturing occurs without limits or deducible patterns--any pattern ceases in the presence of a "counter" designed to discern its objectivity. Nor does Bohr's notion of complementarity suggest a shift in objective representation from the organic or living portrait, no part of which may be inconsequentially removed, to a more schematic outline or constellation, whose absent parts or interstices can be supplied by the mind. Bohr's self-consciously rhetorical, or "novel," formulation of complementarity instead spells out a thoroughly anti-representational logic by which "different experimental arrangements," rather than cohering in any visualizable manner, bring about visibly mutually exclusive results:

    within the scope of classical physics, all characteristic properties of a given object can in principle be ascertained by a single experimental arrangement, although in practice various arrangements are often convenient for the study of different aspects of the phenomena. In fact, data obtained in such a way simply supplement each other and can be combined into a consistent picture of the behavior of the object under investigation. In quantum physics, however, evidence about atomic objects obtained by different experimental arrangements exhibits a novel kind of complementary relationship. Indeed, it must be recognized that such evidence, which appears contradictory when combination into a single picture is attempted, exhausts all conceivable knowledge about the object. Far from restricting our efforts to put questions to nature in the form of experiments, the notion of complementarity simply characterizes the answers we can receive by such inquiry, whenever the interaction between the measuring instruments and the objects forms an integral part of the phenomena. (qtd in Plotnitsky 74)

  11. Like a war which is not one, in that, one-sided, it opposes without measure, a "complementarity" which is not one, in that it represents (or in Bohr's words, "characterizes") the unrepresentable, that which cannot both be and be measured (or known) in "a single picture," recalls, Plotnitsky argues, the irreducible incommensurability that arose along with the first mathematical means for knowing the world, geometry. Perhaps the unilateral assault conducted in the "Science Wars" on a grossly incommensurate object should simply be called, in squarely traditional fashion, "irrational," the negative name given to the algebraic discovery of the immeasurable in geometry. Contradicting contradiction, we may view the true root of the evil signaled by a "war" waged against its own fictional pretext not as the neat opposition of one against one but rather as the original and unsettling complementary relationship that is the base of one with or plus one, an essential and irreducibly intricate twoness like that of mathematics itself under the aspects of algebra and geometry.

  12. For the irrational arose not in opposition to but from within the basic framework of rationality. Exposed to a certain "experimental arrangement," it was discovered, the simplest act of calculation results in an imponderable relation. The most fundamental equation defining physical reality (a_ + b_ = c_), when solved for its simplest values (a=1, b=1) yields, as one of its characteristics, an immeasurable quantity (c= 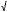2). The root or base number of one with or plus one should represent, in a single picture, an indivisible unity of two. Derivative of that unity as such, more fundamental than the external operation of addition, the common root of two does indeed present "a single picture:" a finite line--the diagonal--delimited by a regular geometric figure. An extension defined by other extensions that together describe a self-containing figure is an entity independent of traditionally symbolic, let alone "novel" complementary relations. Its reality is self-evident, but with an insurmountable hitch: the measure, or mathematical identity, of that reality cannot be figured. Moreover, the necessity of such unattainable knowledge is as pragmatic as it is epistemological. Plotnitsky states its centrality plainly--"one needs it if one wants to know the length of the diagonal of a square"--before explaining how such a novel, or immeasurable, "mathematical object," the irrational ratio, came about:

    13. this is how the Greeks discovered it, or rather its geometrical equivalent. If the length of the side is 1, the length of the diagonal is 2. I would not be able to say--nobody would--what its exact numerical value is. It does not have an exact numerical value in the way rational numbers do: that is, it cannot be exactly represented (only approximated) by a finite, or an infinite periodical, decimal fraction and, accordingly, by a regular fraction--by a ratio of two whole numbers. It is what is called an "irrational number," and it was the first, or one of the first, of such numbers--or (they would not see it as a number) mathematical objects--discovered by the Greeks, specifically by the Pythagoreans. The discovery is sometimes attributed to Plato's friend and pupil Theaetetus, although earlier figures are also mentioned. It was an extraordinary and, at the time, shocking discovery--both a great glory and a great problem, almost a scandal, of Greek mathematics. The diagonal and the side of a square were mathematically proven to be mathematically incommensurable, their "ratio" irrational. The very term "irrational"--both alogon (outside logos) and arreton (incomprehensible) were used--was at the time of its discovery also used in its direct sense. (117-18)

  13. In a very real sense, independent of pretexts visited upon Social Text, it is the "scandal" of the irrational, mathematically and rationally derived, that the so-called Science Wars rehearse, worry, and travesty. Unlike a hoax-based polemic, mathematics publishes and is host to its own "transgression," one "complementary" aspect of its operation excluding another. The discovery that the relationship between the diagonal and side of a square, while governed by the basic Pythagorean theorem regarding the magnitudes of lines composing a triangle, was not translatable into rational mathematical symbols, could not be represented as a ratio of whole numbers, and thus as a rational relationship or (rational) number tout court, was succeeded by the tale of the illustrative death of its progenitor. Legend has it that a storm and resulting shipwreck buried that revolutionary Pythagorean at sea (118-19). Truth may have it that the sound and fury of the "Science Wars," to which The Knowable and the Unknowable tactfully, constructively responds, are an attempt to drown this illustrative figure once more. The storm in which the mythic discoverer of the irrational purportedly met his end may be what this recent tempest in a teapot is attempting, more or less unwittingly, to bring to life again.

  14. Yet, as Plotnitsky makes clear, since the link between the irrational and the rational, the core focus of his book, is borne out specifically by rational processes themselves, the desire to hurl overboard those who articulate the problem of the irrational is tantamount to curtailing rational inquiry itself. In a chapter treating Lacan's "analogous, but not identical" (147) references to the rationally derived imaginary number, the square root of -1, to describe the "irreducibly nonvisualizable" "symbolic object" of his psychoanalytic epistemology--"the 'erectile organ'" or symbolic phallus already operating, according to Lacan, as image or "signifier" in the psyche (141) (Plotnitsky helpfully calls this psychic object "the image of the image of the penis" [110])--Plotnitsky describes how the nonidentities of conceptual analogies function within an epistemological "system":

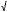    the erectile organ, or, again, a certain formalization of it, must be seen as [...] 'the square root of -1,' (L)-1 of the Lacanian system itself. It is an analogon of the mathematical concept of the mathematical 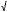-1 within this system, rather than anything identical, directly linked, or even metaphorized via the mathematical square root of -1. In a word, the erectile organ is the square root of -1, which I here designate as the (L)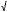-1, of Lacan's system; the mathematical 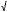-1 is not the erectile organ. (147)

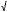    (Plotnitsky explicitly uses the symbol for the mathematical concept 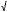-1, and the words "the square root of -1" or the amended "(L)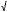-1" to designate the analogous use of that mathematical concept within Lacan's system [113]). In other words, just as 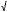-1 is the "simplest complex number," which, "formally adjoined to the old domain of real numbers, enables one to introduce the new domain of complex numbers" (the field of numbers of which real and imaginary numbers are both factors), so the "erectile organ" is the simplest complex concept enabling a new domain or field of psychoanalysis, one in which real and imaginary objects are both irreducible factors (122). Whether or not one views this domain as thoroughly "novel" or as already latent in Freud's epistemology, Lacan's exposition of the complex notion of the phallus (as both imaginary and real) does indeed signal a redefinition of the operative field of psychoanalysis. In addition, Plotnitsky emphasizes, "analogous" means just that: "'the square root of -1' of Lacan's statement is, I shall argue here, in fact not the mathematical 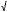-1 [...]. There is no mathematics in the disciplinary sense in Lacan's analysis" (147).

  15. It is in this context of restating the fundamental rational concept and operation of analogy itself, the proverbial wheel of reason here not reinvented but patiently redescribed, that Plotnitsky makes the central observation of his book, speaking not only to the inevitable recourse made to analogy in the course of analyzing essentially nonobjective, psychic phenomena, but to the necessary processes of symbolization and analogy involved in every new discovery of the irrational. Just as "the nonclassical epistemological component may be irreducible in all mathematics" (130), so

    16. irrationality--the inaccessibility to rational representation (in whatever sense)--can itself be discovered rationally, for example and in particular, by means of mathematical proof, a paradigmatic rational argument. This emergence of the irrational (the inaccessible, the unknowable, the unrepresentable, the incomprehensible, the inconceivable, and so forth) at the limit of the rational (the accessible, the knowable, the representable, the comprehensible, the conceivable, and so forth), defines the project of philosophy throughout its history, from Anaximander to Heidegger and beyond, or in mathematics from the Pythagoreans and the diagonal to Gödel and undecidability. In the wake of Heidegger, or indeed Nietzsche, who understood this epistemology more profoundly than anyone before him (and at least as profoundly as anyone since him), the extraordinary critical potential of this situation has been powerfully utilized by such nonclassical thinkers as Bataille, Blanchot, Levinas, Lacan, Derrida, and de Man, or of course Heisenberg and Bohr in the case of quantum mechanics. Indeed, the nonclassical epistemology of quantum mechanics, as considered here, gave especially remarkable shape to these relationships. (119-20)

  16. Plotnitsky's none-too-delphic message is that the irrational indicated by numerical and notational as well as discursive epistemologies, by mathematicians and physicists as well as philosophers, is not going to sink with any single message-bearer to the ocean floor. And again, it is complex mathematics, rather than unilateral polemics, which may best "illustrate" his point. As Bohr rewrites the traditional notion of "complementarity" to indicate and encompass the notion of the noncomplementary, the mutually exclusive realities of a single physical phenomenon viewed under different aspects, so in mathematics the extraordinary notion of complex numbers encompasses both real and imaginary in a single mathematical "field." "Complex" here even appears analogous to "complementary" when the problem of the visualization or spatial representation of such numbers is posed. For, like the mutually exclusive visual evidence provided by differing experimental set-ups in quantum mechanics, the field of complex numbers in mathematics is "symbolically" configurable on a two-dimensional real plane, one of whose axes, however, is being used to represent imaginary numbers. Yet this "schematic illustration," "diagram," or "representation" (on a real plane redefined as the Argand plane), even as it produces a kind of visualization of its objects, and even though its relationship to the field of alegebraic formulation is exhaustive, in no way corresponds to the measurable lengths of real lines or vectors, or the rationally derived points on a line, that real and rational numbers represent. The gap between algebra and geometry, or notation and spatial representation, is thus encompassed within the field of complex (real and imaginary) numbers, but not bridged. The algebra involved must be plotted on two visually analogous but mathematically different ("nonisomorphic") structures: that of the "real plane" (or "vector-space") and the strictly speaking non-spatial "field of complex numbers, which would no longer allow us to see [the real plane] [...] as a real plane" (125-26).

  17. Complex numbers thus produce a "field" irreducible to a "space." The attempt to so reduce the field would result, one might say, in a hoax, the representation of imaginary numbers as real. By analogy one may say that if the real aim of the wagers of the "Science Wars" is to clear the space of rational science of its false representation, that aim will continue to prove itself, in the philosophical sense, "imaginary"--first, because it lacks a real object (let alone enemy), and, second, because in the absence of such, it proves itself to belong foremost to the complementary relations of discourse, that other field in whose complex, nonvisualizable formulations the real and the imaginary, as in mathematics, interact.

  18. Riddled with their own characteristic patterns of misappropriation and misstatement, imaginary acts of salvation may finally not be evidence of ignorance, intellectual disingenuousness, or even analytic bad faith (cf.160-62 especially). The "failure" to "win" a war of one's own invention may instead be analogous to the very force that war would mime: the roiling sea in which (again, as discourse, or legend, would have it) the rational voice of the irrational sinks. That is to say, the war waged upon philosophy may be a certain view of science at war with another view, a rejection of Bohr's conception of complementarity, or the construction of the Gauss-Argand plane, or any articulation of complexity in which one of many "different aspects" is not and cannot be made present. For, in mathematics as in discourse, the irrational and the imaginary are based in the rational and the real they negate. This real scandal, recognized and interpreted in novel terms by traditionally classical proto-modernists (first among them Descartes) no less than nonclassical "post-modernists," may necessarily attract discursive waves of submergence, interpretive storms stirred upon an open sea. Its details may be worth fighting over, but it itself is not open to debate. And the drawing of a bull's eye on one contemporary French thinker or another may be a greater extravagance than any that such contrived aim-taking supposedly targets. Giving a face to the enemy is as old a discursive procedure as the first history of (irrational) war, told with unsparing rationality by Thucidydes. But the weight of tradition does not make this rhetorical maneuver any more substantial, any less imaginary, or, in its "defenses" of rationality, any less incommensurate or irrational.

  19. It is not that the target is moving and hard to hit; it is that it is not what one represents it to be, that objective absence being its very reason, its rationale, for being thought. Such a surmise indeed "characterizes" much "nonclassical" thinking, in which the failure of representation to meet its mark is directly or indirectly addressed. But it is also the irreducible basis for thinking proffered by the two central, significantly different founders of modern classical philosophy, Descartes and Kant, whose respective skeptical and critical limitations of rational cognition, accompanied by a redefinition of the real status of geometry, negatively re-established the novel project and possibility of thought.

  20. The irreducible evidence of the irrational, rationally recognized up to a limit, unites modern mathematics, science, and philosophy into a field whose different aspects may be analogous with complexity itself, complexity which is real and rationally conceived precisely because its elements and factors include the imaginary and the irrational. And it is here, in its recognition of a shared complexity, that Plotnitsky's work takes its most important turn. For, instead of "wars" waged by ventriloquism, Plotnitsky suggests, a mutually reflexive acknowledgement of cognitive limits, the very limits that compose complexity, can include ethical action among its unknowable effects:

    21. perhaps the ultimate ethics or (since the ultimate ethics may not be possible, classically, in practice and, nonclassically, in principle) at least a good ethics of intellectual inquiry, or of cultural interaction, is the following: being strangers ourselves, to offer other strangers, strangers in our own or in other cultures, those ideas that bring our own culture--say, science, on one side, and the humanities, on the other--to the limits of both what is known and unknown, or unknowable, to them. To have an expertise is to reach the limits of both what is knowable and what is unknowable in one's field; and to be ethical in intellectual exchange is to offer others the sense of both of these limits, to tell the other culture or field both what we know and what we do not know ourselves, and what is knowable and what is unknowable, in our own field or culture. (240)

  21. Is this process of "exchange" of "expertise" more complex than attacking an adversary of one's own devising? Doubtless--as the terms themselves suggest, the rational analysis of the irrational cannot, by definition, be unilateral; any such analysis must recognize both its own limits and its relation to what it is not. Yet, as the appearance of The Knowable and the Unknowable demonstrates, even the (irrational) negation of exchange issues in its own negation, or exchange. Thus it is, as Plotnitsky's double expertise confirms, that a certain discrepancy of thinking remains, with the effect that, no more than do Titans, do Lilliputians need fear their final overthrow.

    22. Department of Comparative Literature
    Princeton University
    cblacour@princeton.edu

    Talk Back

    COPYRIGHT (c) 2003 BY Claudia Brodsky Lacour. READERS MAY USE PORTIONS OF THIS WORK IN ACCORDANCE WITH THE FAIR USE PROVISIONS OF U.S. COPYRIGHT LAW. IN ADDITION, SUBSCRIBERS AND MEMBERS OF SUBSCRIBED INSTITUTIONS MAY USE THE ENTIRE WORK FOR ANY INTERNAL NONCOMMERCIAL PURPOSE BUT, OTHER THAN ONE COPY SENT BY EMAIL, PRINT OR FAX TO ONE PERSON AT ANOTHER LOCATION FOR THAT INDIVIDUAL'S PERSONAL USE, DISTRIBUTION OF THIS ARTICLE OUTSIDE OF A SUBSCRIBED INSTITUTION WITHOUT EXPRESS WRITTEN PERMISSION FROM EITHER THE AUTHOR OR THE JOHNS HOPKINS UNIVERSITY PRESS IS EXPRESSLY FORBIDDEN.

    THIS ARTICLE AND OTHER CONTENTS OF THIS ISSUE ARE AVAILABLE FREE OF CHARGE UNTIL RELEASE OF THE NEXT ISSUE. A TEXT-ONLY ARCHIVE OF THE JOURNAL IS ALSO AVAILABLE FREE OF CHARGE. FOR FULL HYPERTEXT ACCESS TO BACK ISSUES, SEARCH UTILITIES, AND OTHER VALUABLE FEATURES, YOU OR YOUR INSTITUTION MAY SUBSCRIBE TO PROJECT MUSE, THE ON-LINE JOURNALS PROJECT OF THE JOHNS HOPKINS UNIVERSITY PRESS.

    Works Cited

    Gross, Paul R., and Norman Levitt. Higher Superstition: The Academic Left and Its Quarrels with Science. Baltimore: Johns Hopkins UP, 1994.

    Macksey, Richard, and Eugenio Donato, eds. The Structuralist Controversy. Baltimore: Johns Hopkins UP, 1970.

    Plotnitsky, Arkady. Complementarity: Anti-Epistemology after Bohr and Derrida. Durham, N.C.: Duke UP, 1994.

    ---, and Richard Crew. "Exchange." Postmodern Culture 8.2: January 1998. </wip/issue.198/8.2exchange.html>

    Sokal, Alan. "Transgressing the Boundaries--Toward a Transformative Hermeneutics of Quantum Gravity." Social Text (Spring/Summer) 1996: 217-52.

    ---, and Jean Bricmont. Fashionable Nonsense: Postmodern Intellectuals' Abuse of Science. New York: Picador, 1998.

    ---, and Jean Bricmont. Impostures intellectuelles. Paris: Odile Jacob, 1997.

    Weinberg, Steven. "Sokal's Hoax." The New York Review of Books 8 Aug. 1996: 11-15.

    ---. "Sokal's Hoax: An Exchange" The New York Review of Books 3 Oct. 1996: 54.

    ---. "Steven Weinberg Replies." The New York Review of Books 3 Oct. 1996: 54.

LINKS: Non-Graphical Users See Top of Page